機械検査 実技学科 問題8
機械検査で出てきそうな問題を作りました。
図はWindowsのペイントを使って手作りなので見にくい部分もありますが、解答はできます。
ぜひチャレンジしてください！！！
問題
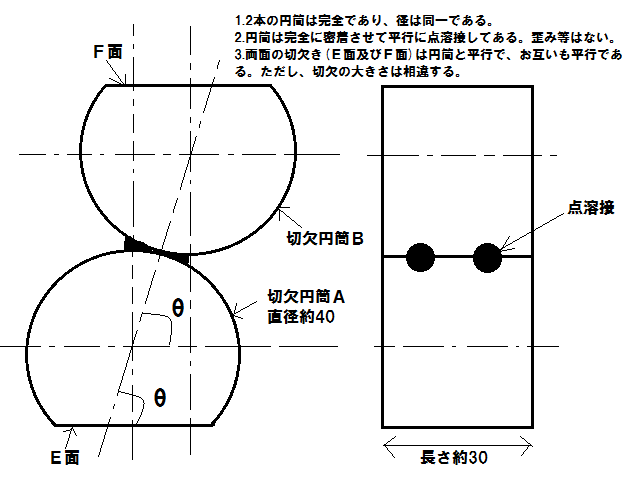
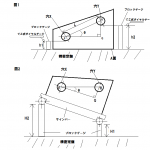
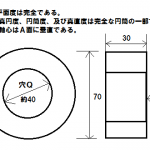
上図に示す部品の中心と切り欠き平面(E面及びF面)のなす角度θを、下記の測定器及び測定用補助具一覧表のみを使用して測定する場合、段取り方法、測段取り図、角度θの計算式を求めてください。
測定器及び測定用補助具一覧表
| 品名 | 寸法又は規格 | 数量 |
| 外側マイクロメータ | 目量0.01mm | 制限なし |
| 測定用ローラ | 16mm 長さ40mm | 2個 |
| 精密定盤 | 1個 |
段取り方法
1.円筒の直径Dを外側マイクロメータで測定する。
2.E面とF面の距離を外側マイクロメータで測りHとする。
3.E面を定盤上に置き、その両側に測定用ローラを当て、外側マイクロメータを使用して測定し、Mとする。
4.3と同様にF面を定盤上に置き、測定用ローラを当て、外側マイクロメータを使用して測定し、Nとする。
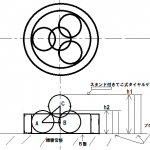
段取り図
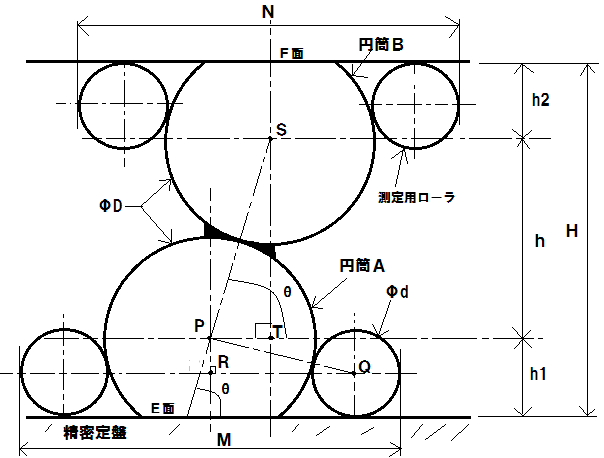
計算式
h1を求める式
△PQRにおいて
\(PQ＝\frac{D}{2}+\frac{d}{2}\)・・・1
\(QR＝\frac{M}{2}-\frac{d}{2}\)・・・2
\(PR＝h1-\frac{d}{2}\)・・・3
三平方の定理より
\(PQ^2＝PR^2+QR^2\)・・・4
4にそれぞれ代入する
\((\frac{D}{2})^2＝(h1-\frac{d}{2})^2+(\frac{M}{2}-\frac{d}{2})^2\)
\(h1＝\sqrt{(\frac{D}{2}+\frac{d}{2})^2-(\frac{M}{2}-\frac{d}{2})^2} +\frac{d}{2}\)・・・5
F面を下にした時、h1の式を参考にh2を求める
\(h2-\frac{d}{2}＝\sqrt{(\frac{D}{2}+\frac{d}{2})^2-(\frac{N}{2}-\frac{d}{2})^2}\)\(h1＝\sqrt{(\frac{D}{2}+\frac{d}{2})^2-(\frac{N}{2}-\frac{d}{2})^2} +\frac{d}{2}\)・・・6
よってhの高さは
\(h＝H -h1 -h2\)・・・答え
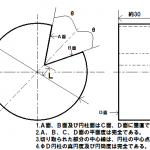
θは△PTSの関係から
\(\sinθ＝\frac{h}{D}\)
\(θ＝\sin ^-1(\frac{h}{D})\)・・・答え
他にも問題作りました。
